Visualisation of the complex roots of y = ax 2 bx c the parabola is rotated 180° about its vertex (orange) Its xintercepts are rotated 90° around their midpoint, and the Cartesian plane is interpreted as the complex plane (green)The vertex of a parabola is the point of intersection of the parabola and its axis of symmetry The quadratic equation has the form ax2 bxc = 0 a x 2 b x c = 0 Sf a a is positive, theWe can convert to vertex form by completing the square on the right hand side;
View Question The Graph Of Y Ax 2 Bx C Is A Parabola With Vertical Axis Of Symmetry The Vertex Of This Parabola Is 2 3 And The Parabola Contain
Vertex of parabola y=ax^2 bx c
Vertex of parabola y=ax^2 bx c-Making b positive or negative only reflects the parabola across the yaxis So, the displacement of the vertex from the yaxis is caused by the absolute value of b Finally, let's look at how changing c affects the graph of the parabola We will look at the graph where c = 3, 2, 1, 0, 1, 2, and 3, a = 1, and b = 3 As we can see from the Show that y = ax 2 bx c, a ≠ 0 represents a parabola and find its vertex, focus, directrix and latus rectum




Quadratic Function Y Ax 2 Bx C Quadratic
Our equation is in standard form to begin with y=ax 2 bxc;The vertex of a parabola y = f(x) = ax^2 bx c (1) or y = f(x) = ax^2 bx (2) or y = f(x) = ax^2 (3) represents the maximum or minimum point on the graph of f To find the maximum or the minimum point, you need to find the derivative f'(x) of the given function and set it to 0Parabola equation can let you calculate the vextex of any parabola in the graph
36 is the value for 'c' that we found to make the right hand side a perfect square trinomial//googl/JQ8NysVertex Formula for the Quadratic Function f(x) = ax^2 bx cY= ax^2 bx c = (4 3^05)*x^2 (4 2* (3^05))*x 4 b) y= ax^2 bx c has vertex (4,1) and passes through (1,11) 1 = 16a 4b c 11 = a b c the vertex is x = b/2a that is b/2a = 4 by solving the system of equations 16a 4b c = 1 a b c = 11 b/2a = 4
See answer below Given a parabola equation If the parabola equation is in the form f(x) = Ax^2 Bx C = 0 The vertex is (B/(2A), f(B/(2A))) Once you have the x value of the vertex, just evaluate the function with that xvalue Example f(x) = 3x^2 2x 9 x = (2)/(2*3) = 2/6 = 1/3 f(1/3) = 3 (1/3)^2 2/1 * 1/3 9 f(1/3) = 3/1 * 1/9 2/3 9 f(1/3) = 3/9 2/3 9 f(1/3) = Standard Form The standard equation of Parabola is y=ax2bxc Vertex Form The Vertex form of the quadratic equation of Parabola is y = (x – h)2 k, here (h,k) are the points on the xaxis and yaxis respectively As we have seen Parabola has two different forms of equations The method to find Vertex is different for both forms ofLearn how to graph a parabola of the form f(x)=ax^2bxc with integer coefficients, and see examples that walk through sample problems stepbystep for



Exploring Parabolas Y Ax 2 Bx C




Graphing Y Ax2 Bx C Youtube
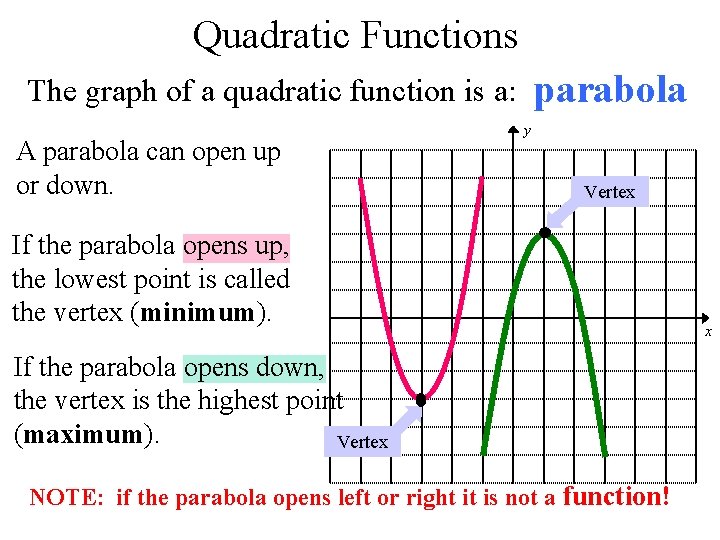
The standard form of a parabola equation is y=ax^ 2 bxc Input the values of a, b and c, our task is to find the coordinates of the vertex, focus and the equation of the directrix The vertex of a parabola is the coordinate from which it takes the sharpest turn whereas y=a is the straightline used to generate the curve So, the coordinates of the vertex are V = (x v , y v) = (5/2 , – 1/4) or (2,5 , 0,25) yaxis interception point The parabola intercepts the yaxis at the value of the c coefficient In the function above, the value of c = 6, therefore, the parabola intercepts the yaxis at the point (0, 6) Graph of a quadratic function As said before, the graph of a quadratic function is known as aThe graph of a quadratic equation in two variables (y = ax2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot We say that the first parabola opens upwards (is a U shape) and the second parabola opens
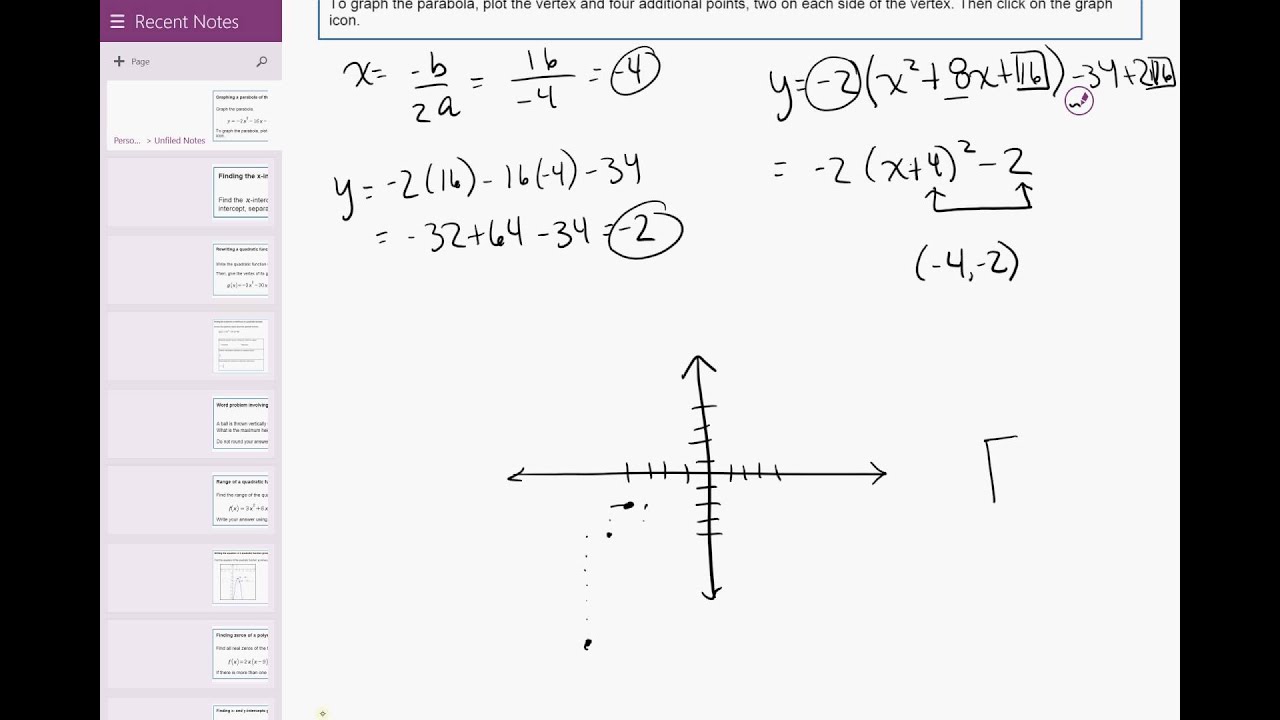



15 04 Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube




View Question The Graph Of Y Ax 2 Bx C Is A Parabola With Vertical Axis Of Symmetry The Vertex Of This Parabola Is 2 3 And The Parabola Contain
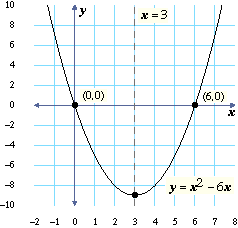
Please Subscribe here, thank you!!!F (x) = ax 2 bx c are given by the quadratic formula The roots of a function are the xintercepts By definition, the ycoordinate of points lying on the xaxis is zero Therefore, to find the roots of a quadratic function, we set f (x) = 0, and solve the equation, ax 2 bx c = 0 We can do this by completing the square as,We want to find the vertex of this parabola The vertex is on the axis of symmetry, so its $x$coordinate is 3 The vertex is also a point on the parabola, so it satisfies the equation for the parabola This means that if you plug the $x$coordinate of the vertex into the equation, you will get the $y$coordinate Plugging 3 for $x$ into $y=x^26x$ gives $y=(3)^26(3)$ → $y=918$



Graphing Quadratic Equations Functions Parabolas By Finding Vertex Worksheet




Graphing Quadratic Functions Y Ax 2 Bx C Quadratic Functions The Graph Of A Quadratic Function Is A Parabola A Parabola Can Open Up Or Down If Pptx Powerpoint
Is it possible to generalize for any function f(x)? Focusing on the standard form of a parabola y = ax 2 bx c and the vertex equation y = a(x – h) 2 k, we can get the first formula of vertex ie The vertex formula will be (h, k) = (b/2a, D/4a) where D = b 2 – 4ac How do you Use Vertex Formula?PARABOLAS TRANSLATIONS AND APPLICATIONS QUADRATIC RELATION A quadratic relation in two variables is a relation that can be written in the form y=ax^2bxc or x=ay^2byc where a, b, and c are real numbers, and a!=0 The graphs of quadratic relations are called parabolas The simplest quadratic relation of the form y=ax^2bxc is y=x^2, with a=1, b=0, and c=0, so this
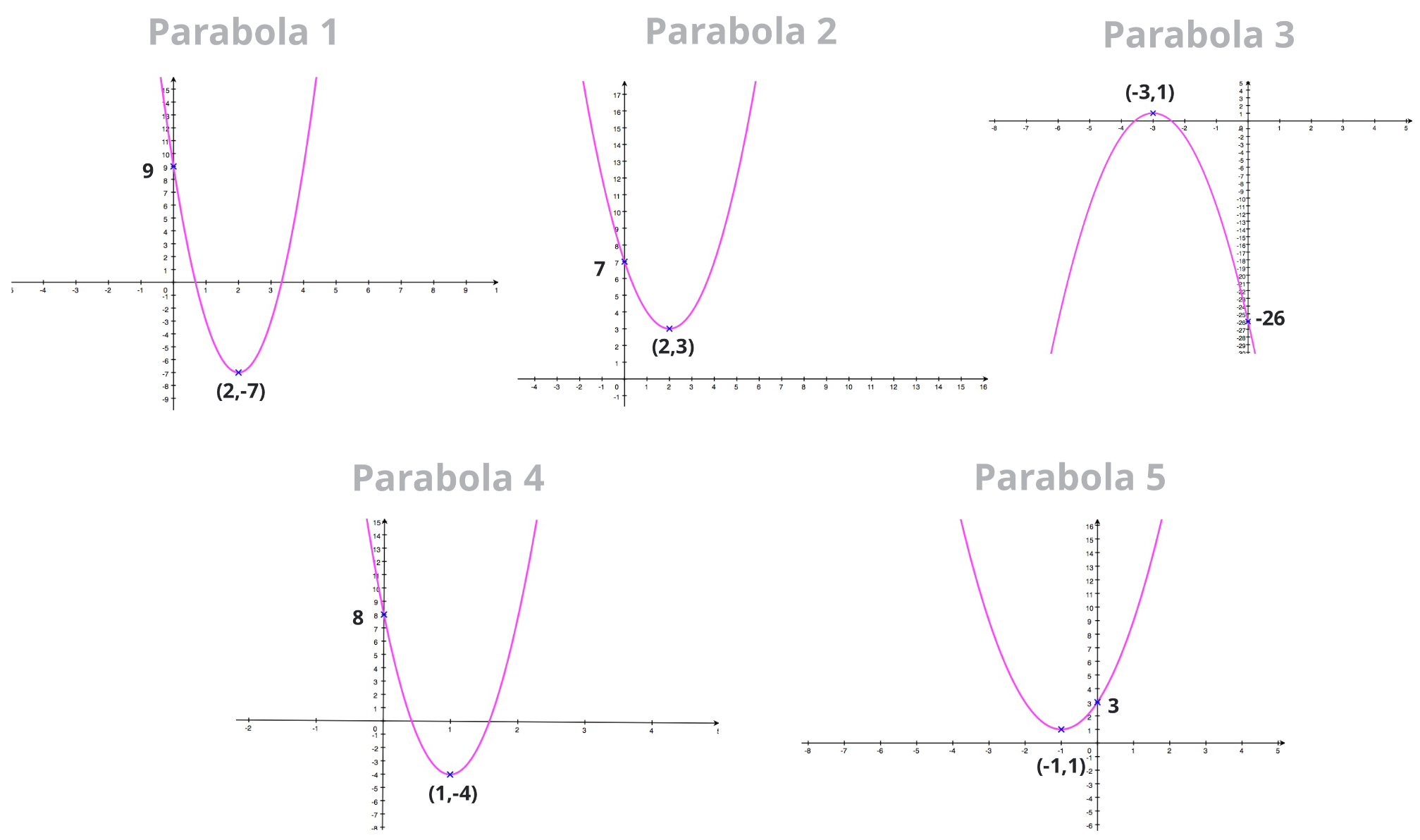



Vertex Form How To Find The Equation Of A Parabola




Quadratic Function Y Ax 2 Bx C Quadratic
y = ax 2 bx c The vertex of a parabola is the coordinate from which it takes the sharpest turn whereas a is the straightline used to generate the curve Focus is the point with is equidistant from all points of the parabola Here, we will find the vertex, focus, and directrix of a parabola There is a mathematical formula that finds allSOLUTION A parabola y = ax^2 bx c has vertex (4, 2) If (2, 0) is on the parabola, then find the value of abcThe general form of a quadratic is "y = ax 2 bx c"For graphing, the leading coefficient "a" indicates how "fat" or how "skinny" the parabola will beFor a > 1 (such as a = 3 or a = –4), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample values
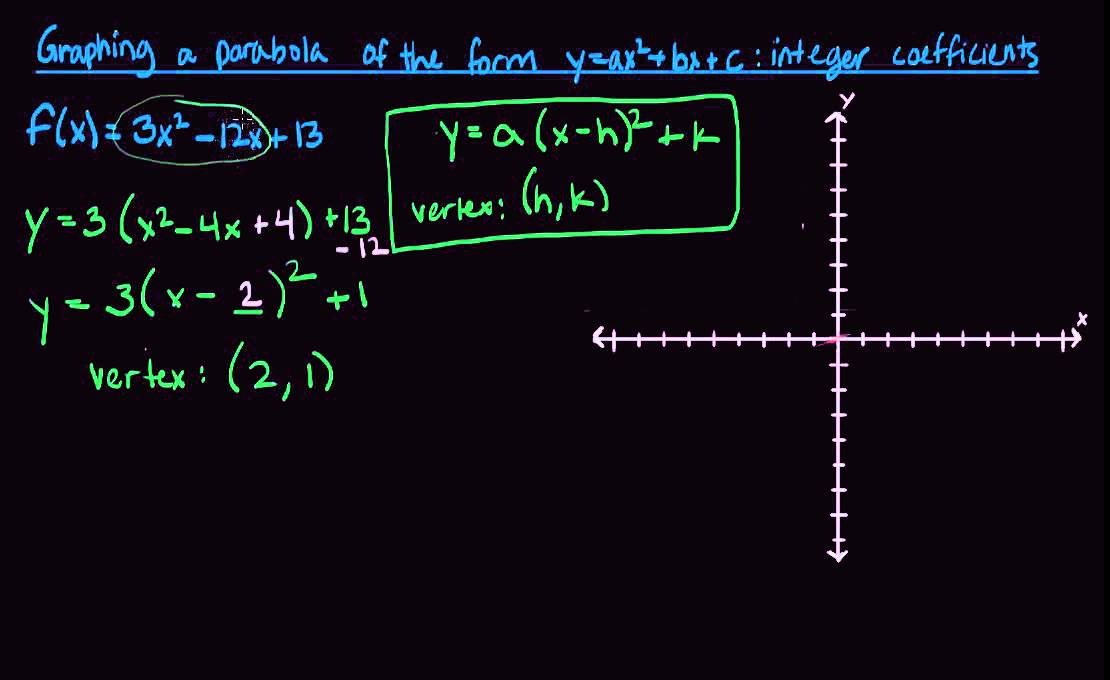



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube



Quadratic Graph Example Y Ax Expii
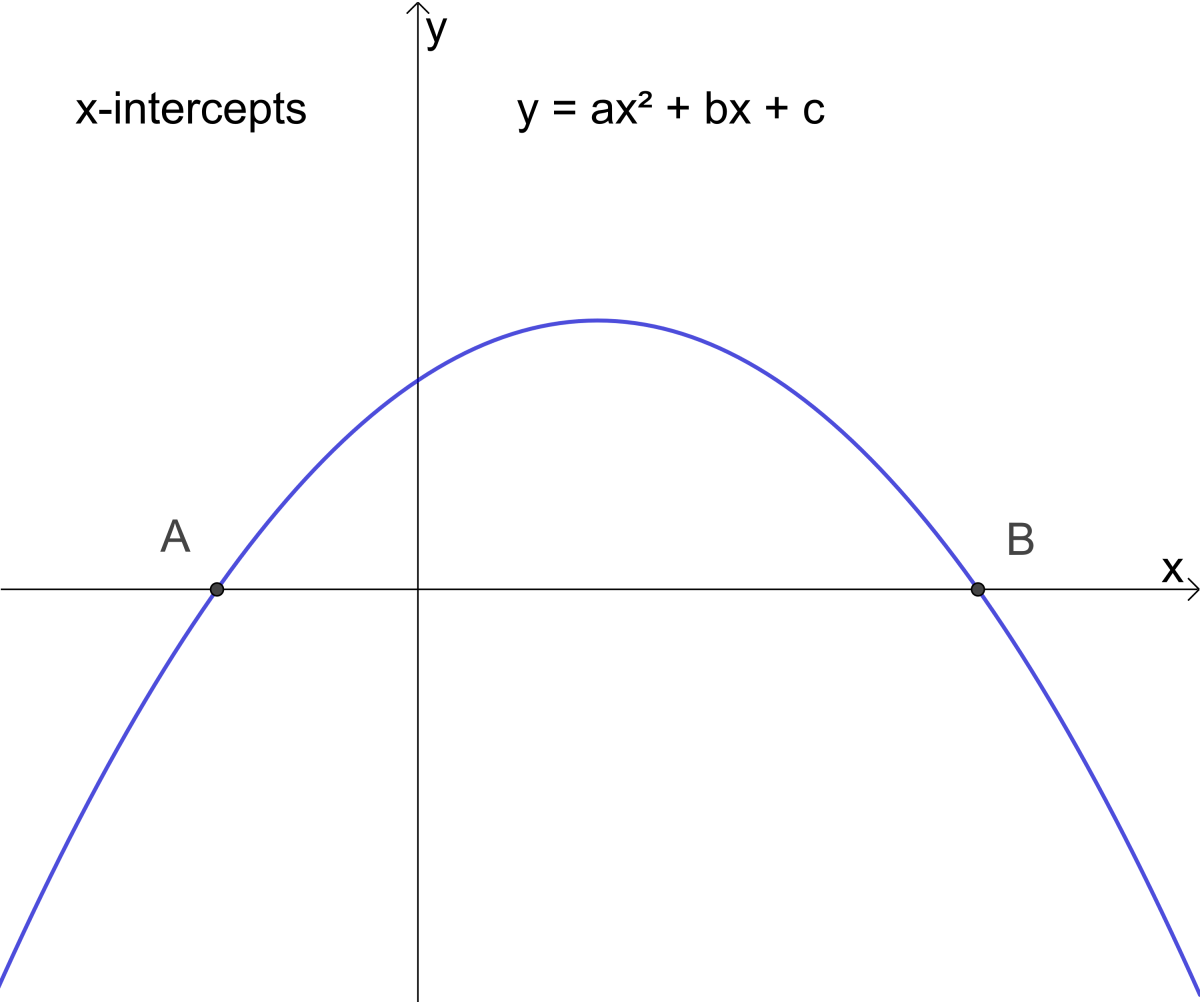
Given a parabola y = a x 2 b x c, the point at which it cuts the y axis is known as the y intercept The y intercept will always have coordinates ( 0, c) where c is the only term in the parabola 's equation without an xAbout Graphing Quadratic Functions Quadratic function has the form $ f(x) = ax^2 bx c $ where a, b and c are numbers You can sketch quadratic function in 4 steps I will explain these steps in following examplesClick here👆to get an answer to your question ️ Suppose a parabola y = ax^2 bx c has two x intercepts one positive and one negative, and its vertex



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego Flip Ebook Pages 1 5 Anyflip Anyflip



2
We learn how to find the equation of a parabola by writing it in vertex form In the previous section, we learnt how to write a parabola in its vertex form and saw that a parabola's equation \y = ax^2bxc\ could be rewritten in vertex form \y = a\begin{pmatrix}x h \end{pmatrix}^2k\ where \(h\) is the horizontal coordinate of the vertex2) The parabola will be shifted up c units when compared to the parabola ax^2 bx 3) The yintercept of the parabola will be f(0) = a*0 b*0 c = c 4) The xintercepts will be when f(x) = 0 Thus, they will happen at the solutions of the quadratic equation You may have 2 intercepts if b^2 4ac > 0, 1 intercept if b^2 4ac = 0, or no Given a parabola having equation y=ax2bxc with a≠0, find the coordinates of the vertex Question Given a parabola having equation y=ax2bxc with a≠0, find the coordinates of the vertex This problem has been solved!



Find The Vertex Of A Quadratic Equation Easily Science Trends




Graphing Quadratics
You can do this graphically, analytically, or even with calculus!While, if it opens downward, the vertex represents the maximum of the function To facilitate finding the vertex, it is often convenient to convert a quadratic equation from standard form , y(x) = ax 2 bx c, to vertex form, y(x) = a(x − h) 2 k, where a ≠ 0You can put this solution on YOUR website!



1




A Parabola Y A X 2 B X C Has Vertex 4 2 2 0 Is On The Parabola Then Abcepuals
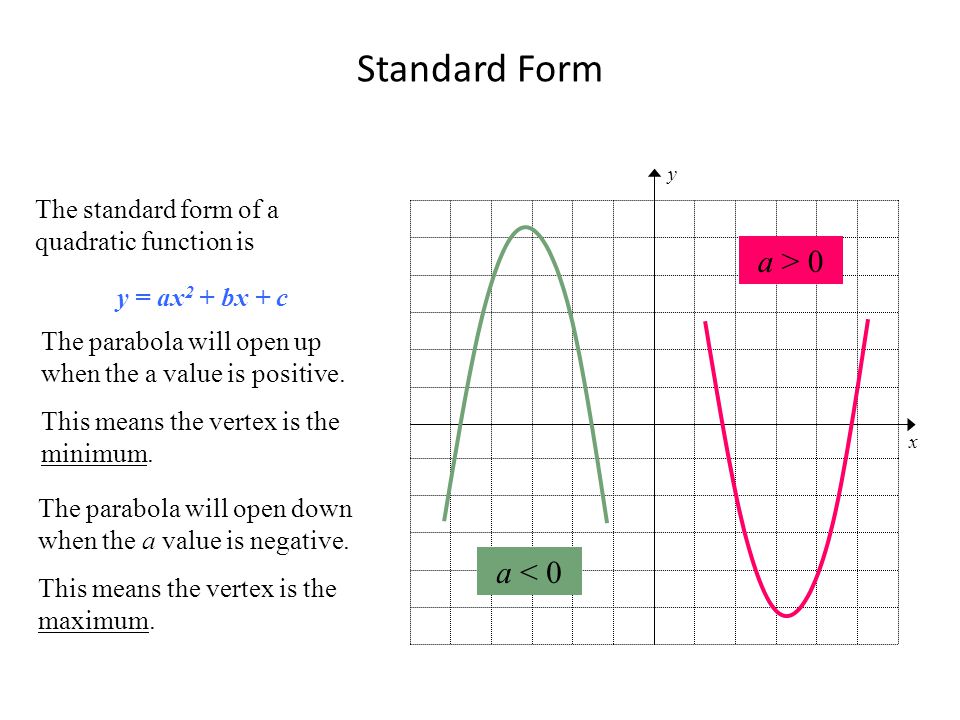
Y = ax 2 bx c or x = ay 2 by c 2 Geometric A parabola is the set of allThe vertex of y = a x 2 b x c Set a = 1, b = − 4, and c = 2 to look at the graph of y = x 2 − 4 x 2 Using the formula x = − b 2 a , you can calculate that the axis of symmetry of this parabola is the line x = 2 Also, notice that the vertex of this parabola is the point ( 2, − 2) Now slide c to 45If the parabola opens upward, the vertex represents the minimum of the function;
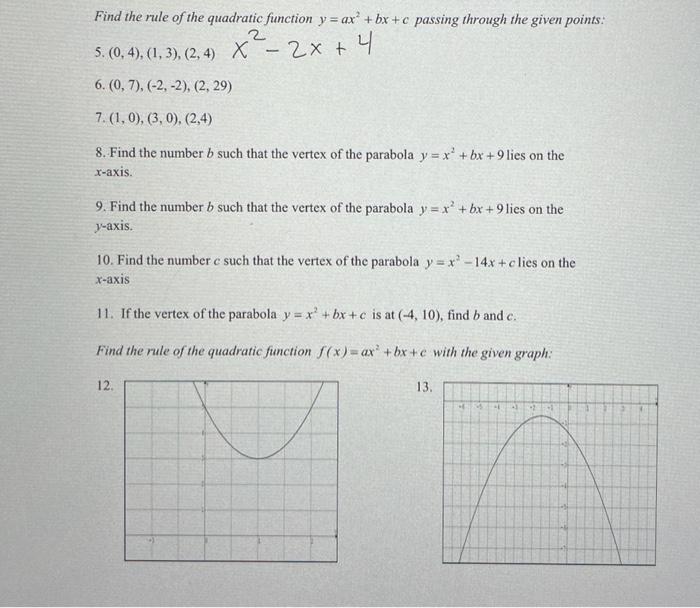



Solved Find The Rule Of The Quadratic Function Y Ax Bx C Chegg Com
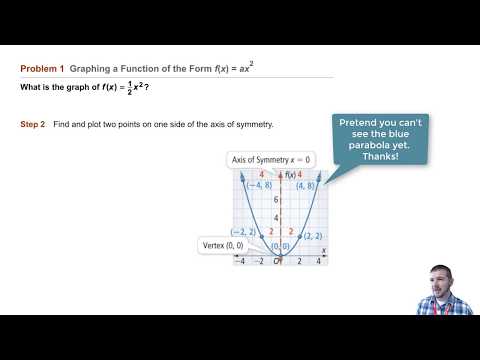



Quadratic Graph Example Y Ax Expii
We want to put it into vertex form y=a(xh) 2 k;We know that the standard form of x) Here, half the coefficient of x is b/2a and its square is b 2 /4a 2 Adding andLearn termquadratics = y = ax^2 bx c with free interactive flashcards Choose from 68 different sets of termquadratics = y = ax^2 bx c flashcards on Quizlet




Quadratic Function



Which Is The Coordinate Of The Vertex Of Y Ax 2 Bx C Quora
How To Find Quadratic Equation From Graph Without Vertex A parabolic equation resembles a classic quadratic equation A quadratic function can be graphed using a table of values Source wwwpinterestcom Another way of finding the increasing or decreasing intervals of quadratic function, is using the algebraic notation of the function (without a graph)The graph of a parabola either opens upward like y=x 2 or opens downward like the graph of y = x 2 In the figure, the vertex of the graph of y=x 2 is (0,0) and the line of symmetry is x = 0 Definition Parabola 1Algebric A Parabola is the graph of a quadratic relation of either form where a ≠ 0;$$$$ Let $y=ax^2 bx c$ Then $y' = 2ax b$ When the slope, ie $y'$, equals zero, the function reaches its vertex Obviously on any graph the tangent line to a parabola's vertex has zero slope Then we can say $$0=2axb$$ $$x=\frac{b}{2a}$$ $\endgroup$ –




The Vertex Of The Parabola Y Ax 2 Bx C Is




Quadratic Function
First let's write down the general form for the vertex of ρ Through any of various means we can find that the x coordinate of the vertex is − b 2 a Substituting this value into the equation for ρ we get that the vertex is ( − b 2 a, c − b 2 4 a) Since the x coordinate of the vertex is linear in b and the y coordinate is quadratic in b (has a b 2 ), we can conclude that the vertexTransform the general equation y=ax^2bxc to vertex form , where the vertex= (h,k) Keep in mind that this was done by a human, when there are only letters and variables involved, I can only do but so much to check myself I checked it against a real quadratic equation in which I could find the vertex If I'm right the x value of the vertex would be Given a parabola #y = ax^2 bx c# find the slope of the parabola at the point (x, y) without using derivatives or any limits?
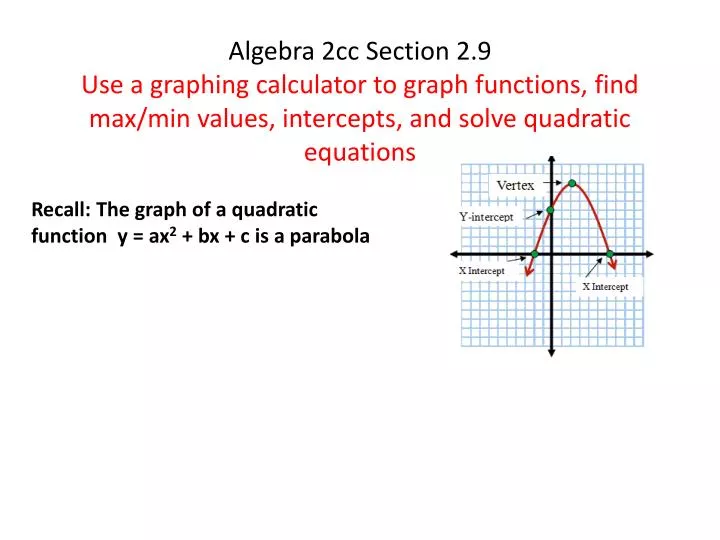



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id
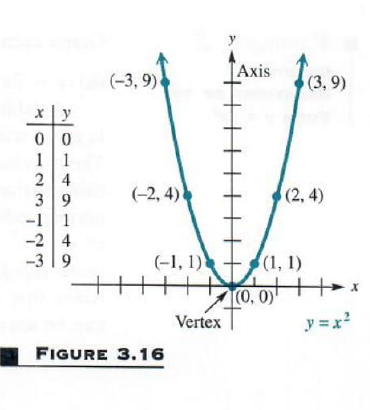



Solve Quadratic Relation Parabolas Step By Step Math Problem Solver
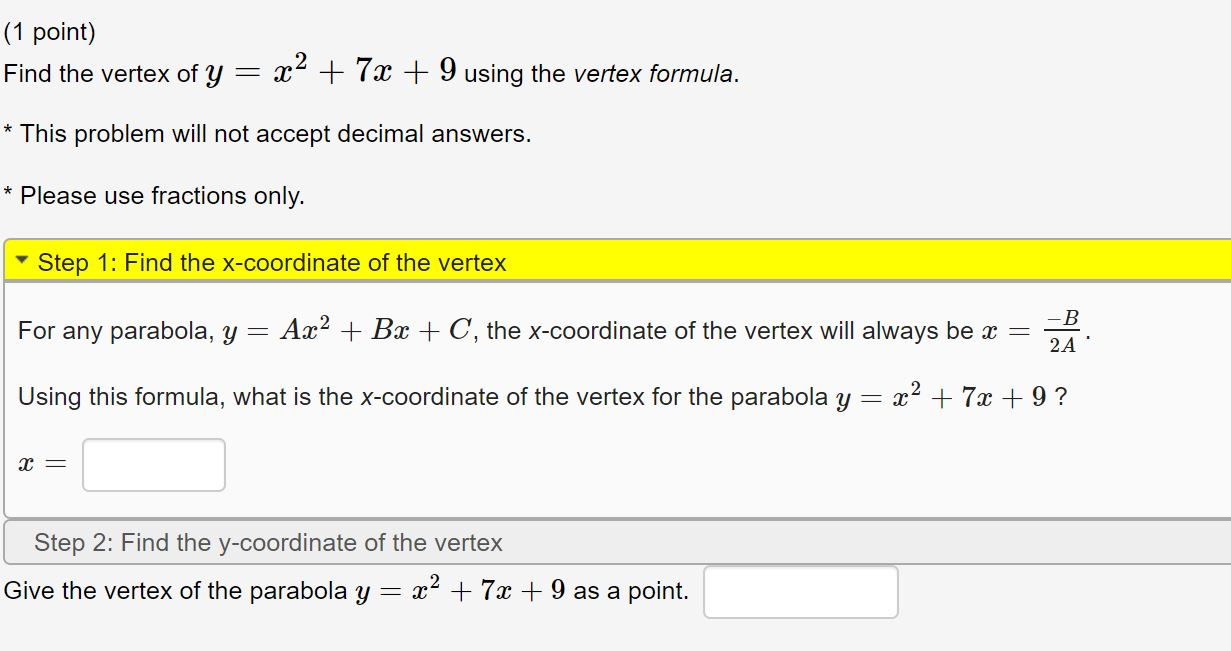
See the answer SeeTo Graph the Quadratic Function \(y = ax^2 bx c\text{}\) Determine whether the parabola opens upward (if \(a \gt 0\)) or downward (if \(a \lt 0\)) Locate the vertex of the parabola The \(x\)coordinate of the vertex is \(x_v =\dfrac{b}{2a}\text{}\)1 1 If the vertex of the parabola y = x' bx c is at (4, 10), find b and c Find the rule of the quadratic function f ( x) = ax bx c with the given graph 12




Quadratic Function Wikipedia




Graphing Parabolas
Find abc if the graph of the equation y=ax^2bxc is a parabola with vertex (5,3), vertical axis of symmetry, and contains the point 0Into the standard form of a quadratic function, y = ax2 bx c In general, any equation for a parabola that can be written in the vertex form yk = a(x h)2 can be rewritten in the standard form y = ax2 bx c Example 1 Show that the equation y 16 = 3(x 5)2 can be rewritten in the form y = ax2 bx c, and give the values of a, b, and cSince the vertex is a useful point we can complete the square to convert ax 2 bx from AA 1



If Distance Between Vertex And Focus Of The Parabola Y Ax 2 Bx C Is Unity Then Value Of A Is Sarthaks Econnect Largest Online Education Community
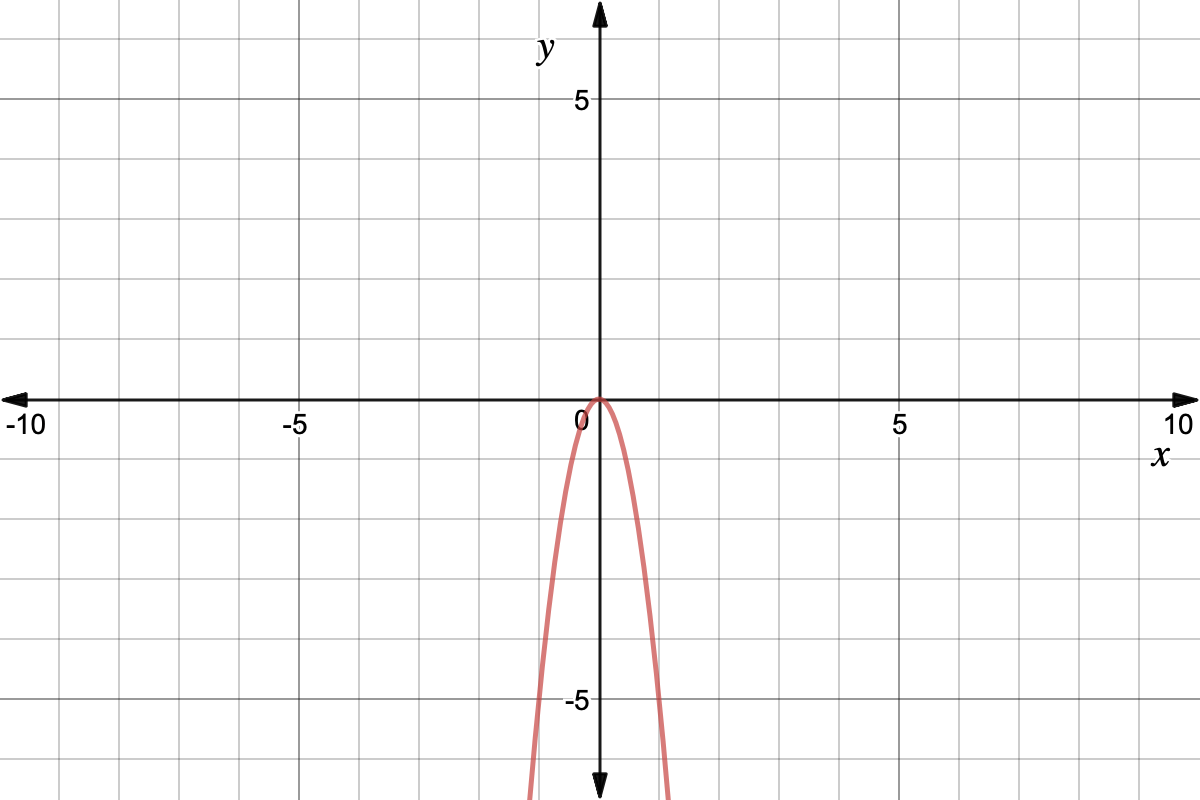



Quadratic Graph Example Y Ax Expii
Y = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, y To find the vertex of a quadratic equation, y = ax2 bx c, we find the point (b / 2a, a(b / 2a)2 b(b / 2a) c), by following these steps Get the equation in the form y = ax2 bx c Calculate –b / 2a This is the xcoordinate of the vertex To find the ycoordinate of the vertex, simply plug the value of –b / 2a into theExploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third




Solved Prove That The Graph Of The Parabola Y Ax 2 Bx Chegg Com



If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community



Investigating Y Ax 2 Bx




Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola



Find The Vertex Of Y X2 2x 8 Using The Vertex Form Gauthmath




Solved Question 6 Find The Vertex H K Of The Parabola 2x 8 X 6 H K Question 7 Rewrite The Parabola Y 3 X 4 2 3 In The Form Y Ax Bx C



Solution A Parabola Y Ax 2 Bx C Has Vertex 4 2 If 2 0 Is On The Parabola Then Find The Value Of Abc



Topic U2 L1 Parts Of A Quadratic Function Graphing Quadratics Y Ax 2 Bx C Eq Can I Identify The Vertex Axis Of Symmetry X And Y Intercepts Ppt Download



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego Flip Ebook Pages 1 5 Anyflip Anyflip




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download



Solved 1 Point Find The Vertex Of Y 63 2 Using The Vertex Chegg Com
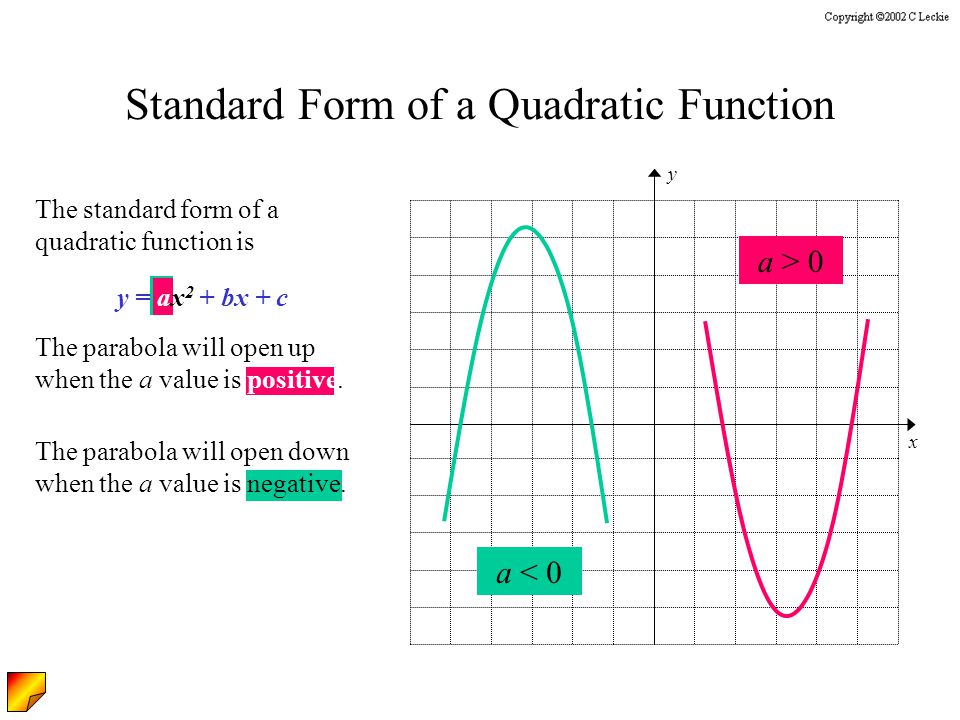



Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download



1
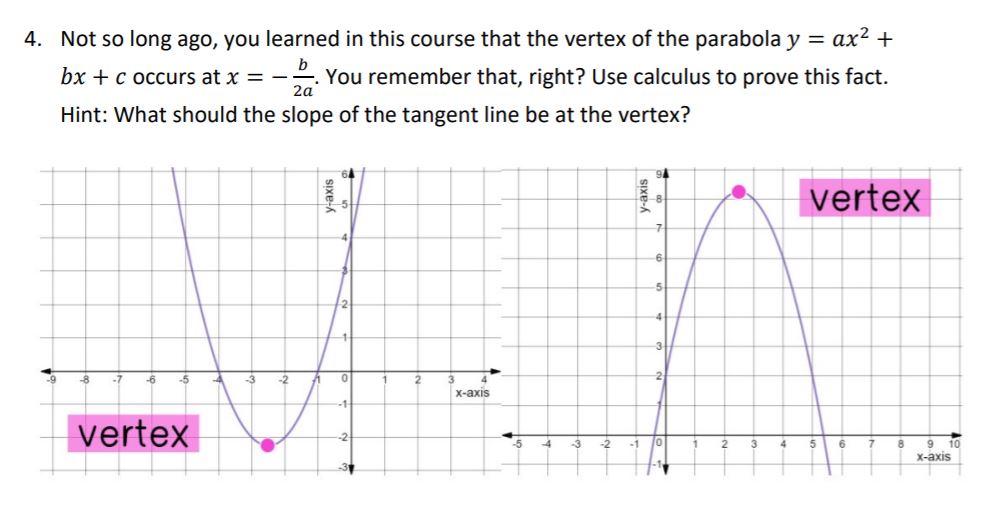



Answered Not So Long Ago You Learned In This Bartleby




Suppose That A Parabola Y Ax 2 Bx C Where A 0 And A B



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Sarthaks Econnect Largest Online Education Community



1
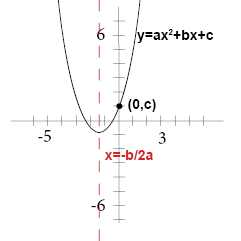



How Do You Graph F X 3x 2 4x 1 Socratic
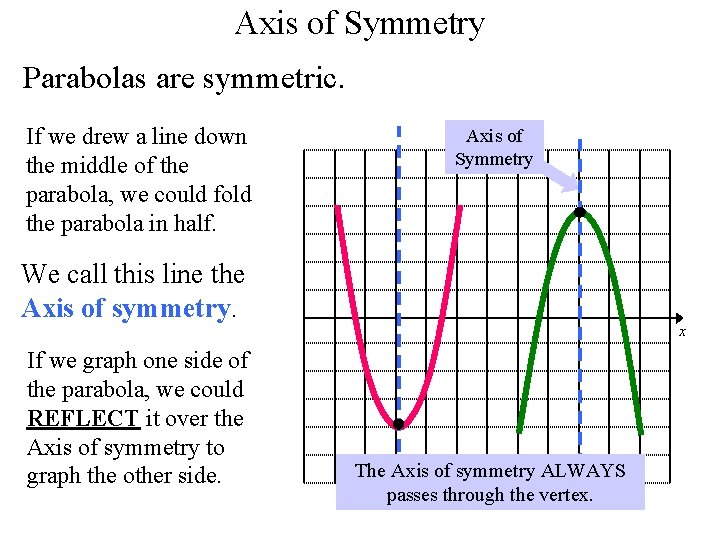



Quadratic Function Y Ax 2 Bx C Quadratic




Finding The Parts Of A Parabola Ck 12 Foundation




Focus Of Parabola Y Ax 2 Bx C Is



Finding A Quadratic Function With A Parabola Studypug



Lessons 5




Consider The General Quadratic Function F X Ax 2 Bx C With A Is Not Equal To 0 A Find The Coordinates Of The Vertex In Terms Of A B And



Unique Quadratic Equation In The Form Y Ax 2 Bx C




1 The Standard Form Of A Quadratic Equation Is Y Ax 2 Bx C 2 The Graph Of A Quadratic Equation Is A Parabola 3 When A Is Positive The Graph Opens Ppt Download




The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com
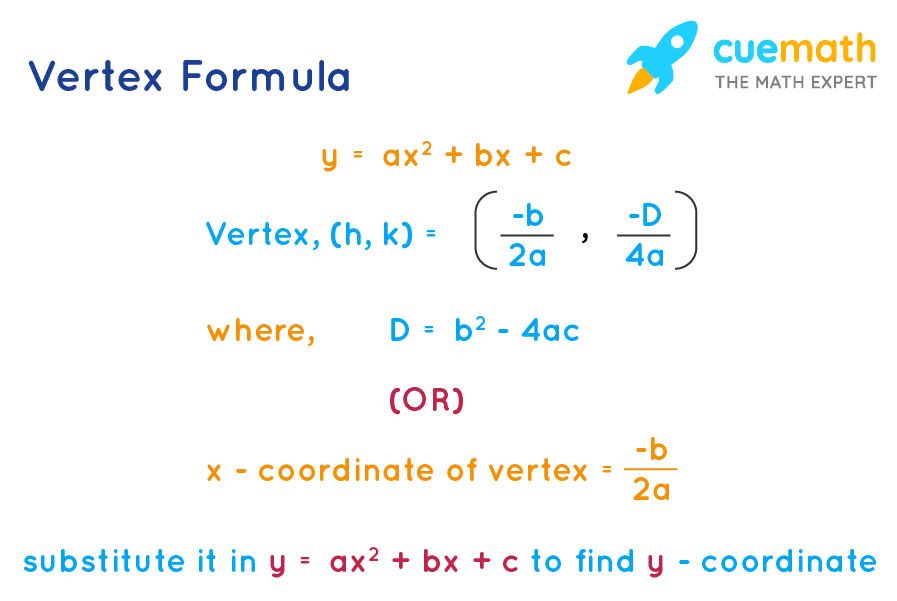



Vertex Formula What Is Vertex Formula Examples
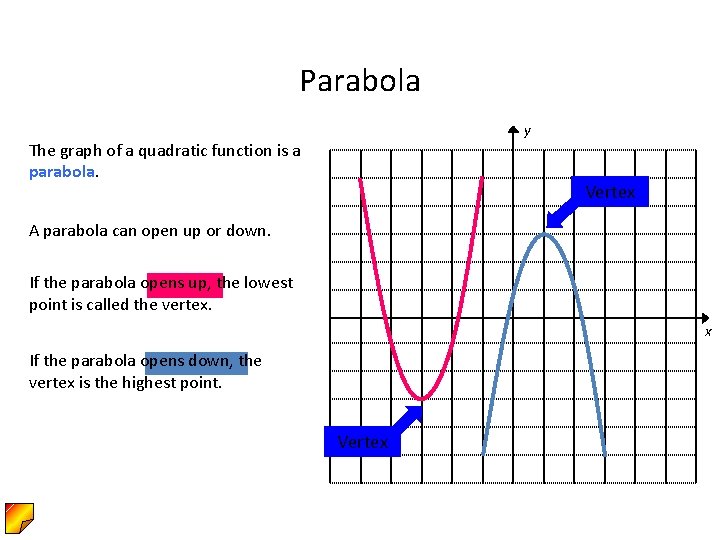



Graphing Quadratic Functions Y 2 Ax Bx C



Which Is The Coordinate Of The Vertex Of Y Ax 2 Bx C Quora
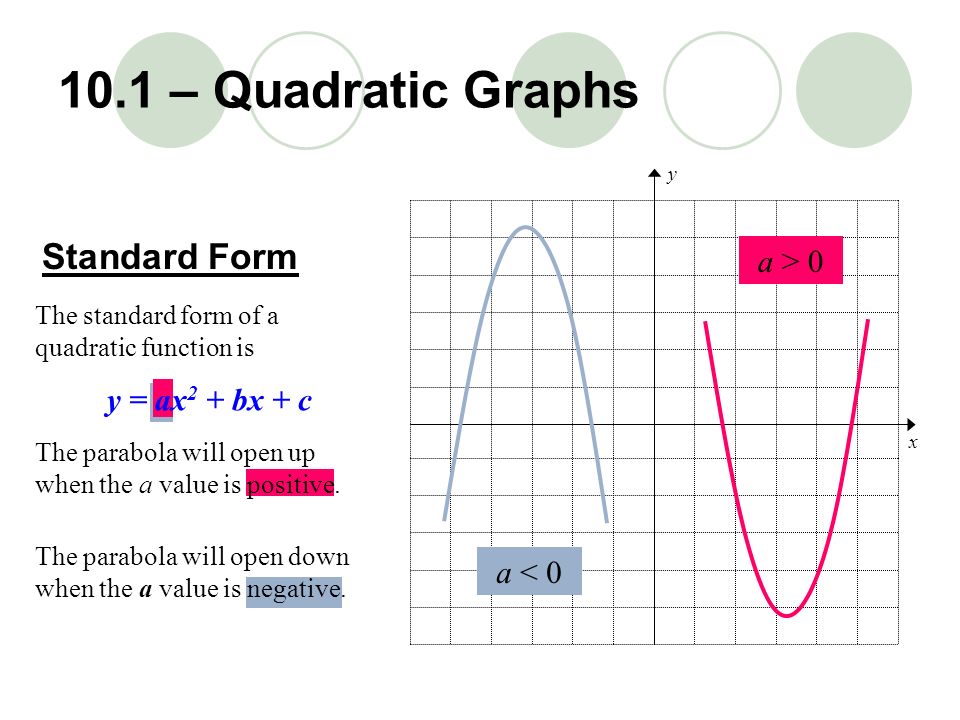



10 1 Quadratic Graphs Ppt Download
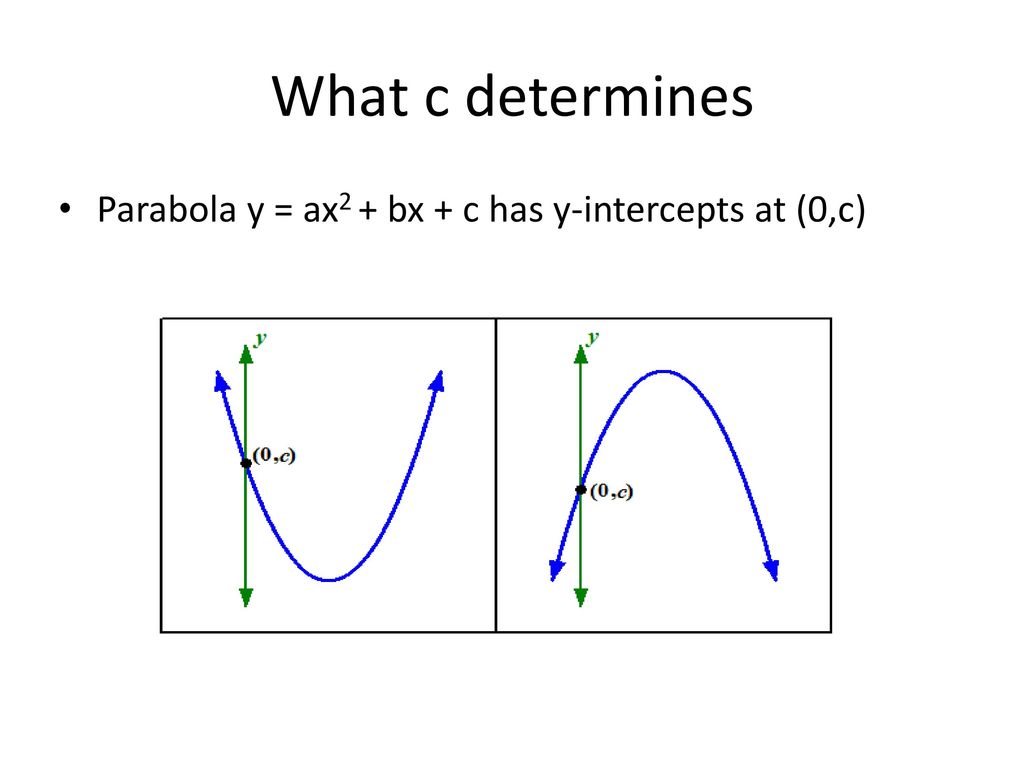



How To Draw A Parabola Ppt Download




Finding The Vertex Of A Parabola In Standard Form Video Khan Academy
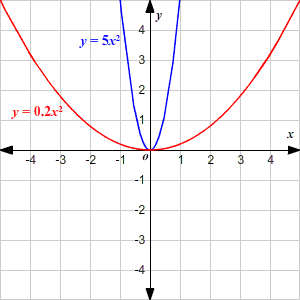



Parabolas




Graphing Quadratic Functions Y Ax 2 Bx C



Math Hawaii Edu



Y Ax2 Bx C Equation




Solved The Vertex Of The Parabola Y Ax 2 Bx C Has Chegg Com



How To Find And Graph The Vertex Axis Of Symmetry Focus Directrix And Direction Of Opening Of The Parabola Given These Equations I 4 Y 2 X 4 2 Ii Y 8 2 4 X 4 And Iii Y 1x 2 2 3x 19 2
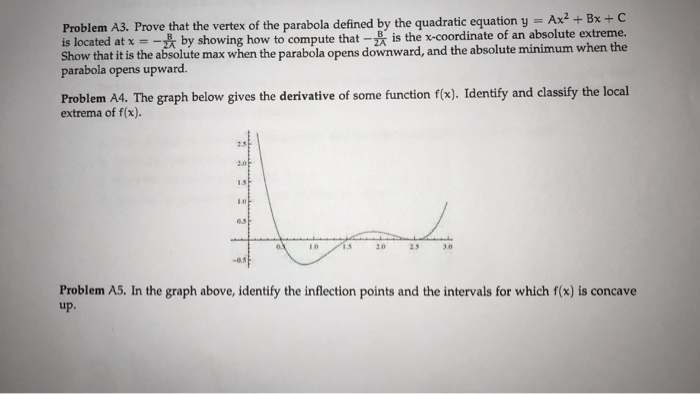



Solved Problem A3 Prove That The Vertex Of The Parabola Chegg Com




Graphing Y Ax 2 Bx C
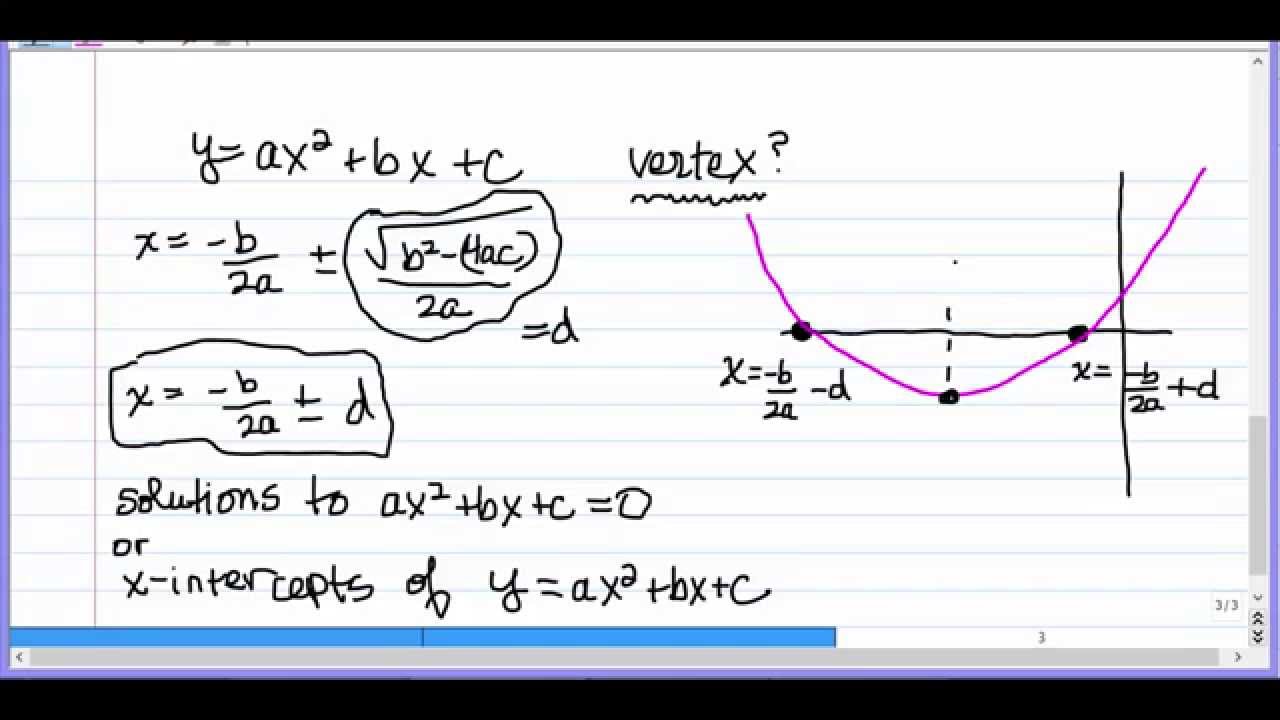



Finding The X Coordinate Of The Vertex Of A Parabola Youtube




Axis Of Symmetry Of A Parabola



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Graphing Y Ax 2 Bx C



How To Determine The Values Of A And B In Relation To Y Ax 2 Bx 8 If The Vertex Is Located At 1 7 Quora



Why Is The Vertex Of A Parabola Is B 2a D 4a Where D B 4ac Quora
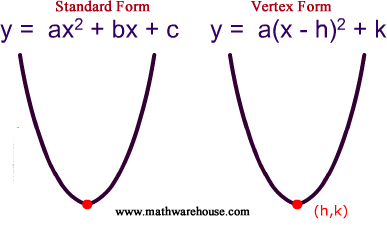



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph




Quadratic Function
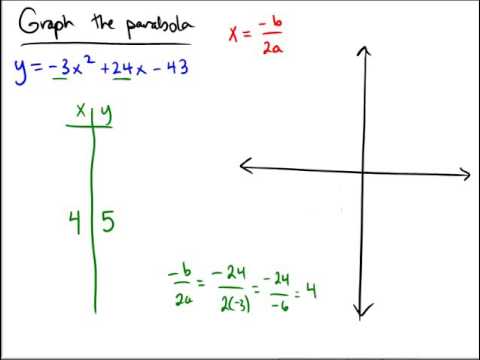



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube
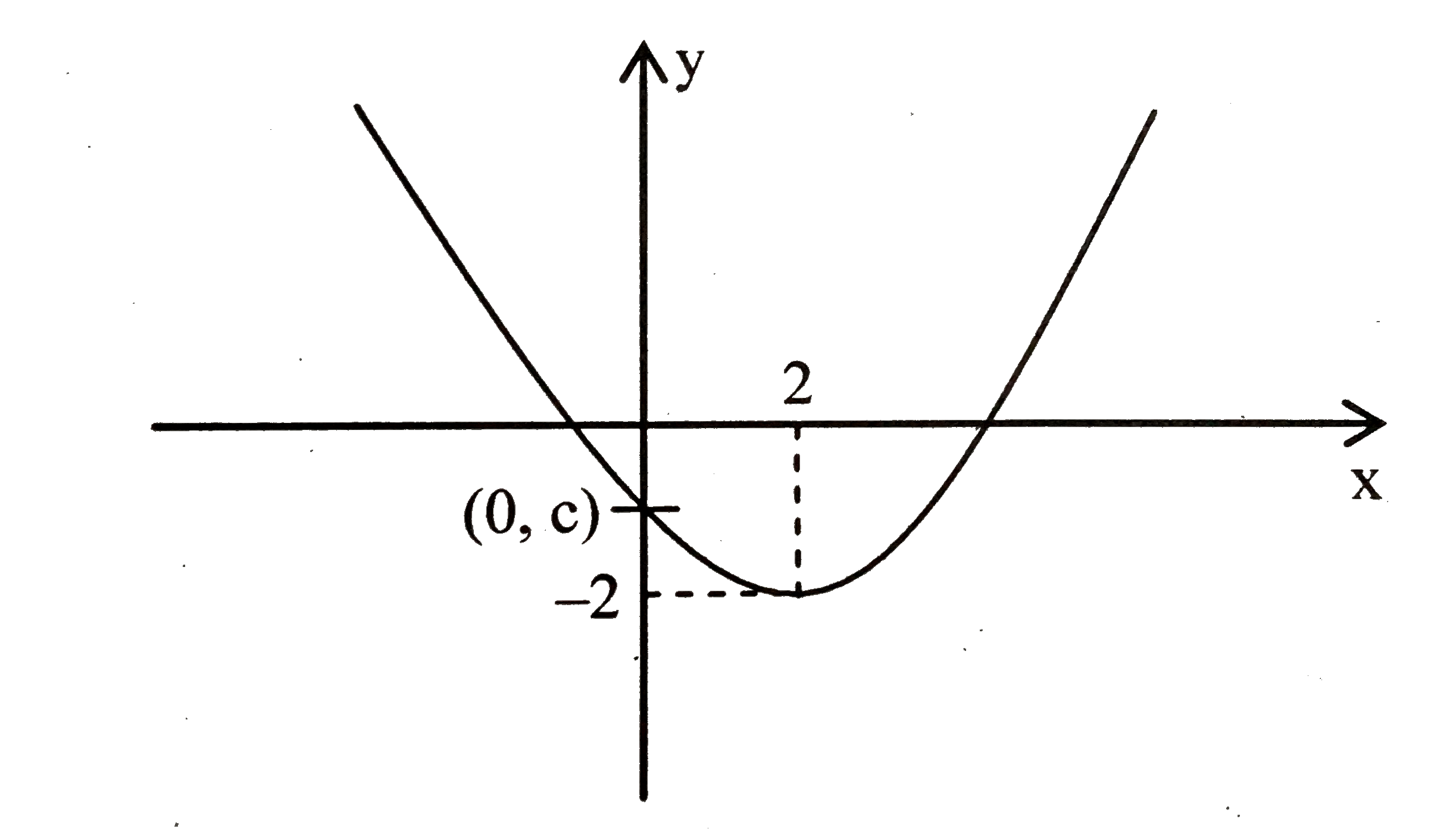



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Then Which Of The Following Is True A Ab 0 B
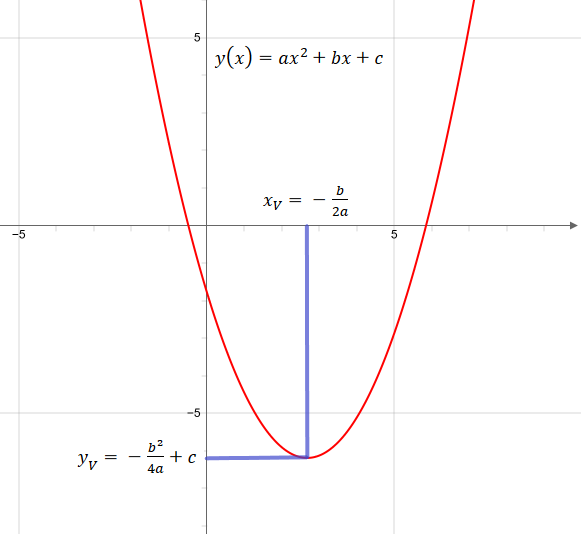



Online Calculator For Converting Quadratic Equation From Normal Form To Vertex Form



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora



Quadratic Function Y Ax 2 Bx C Quadratic
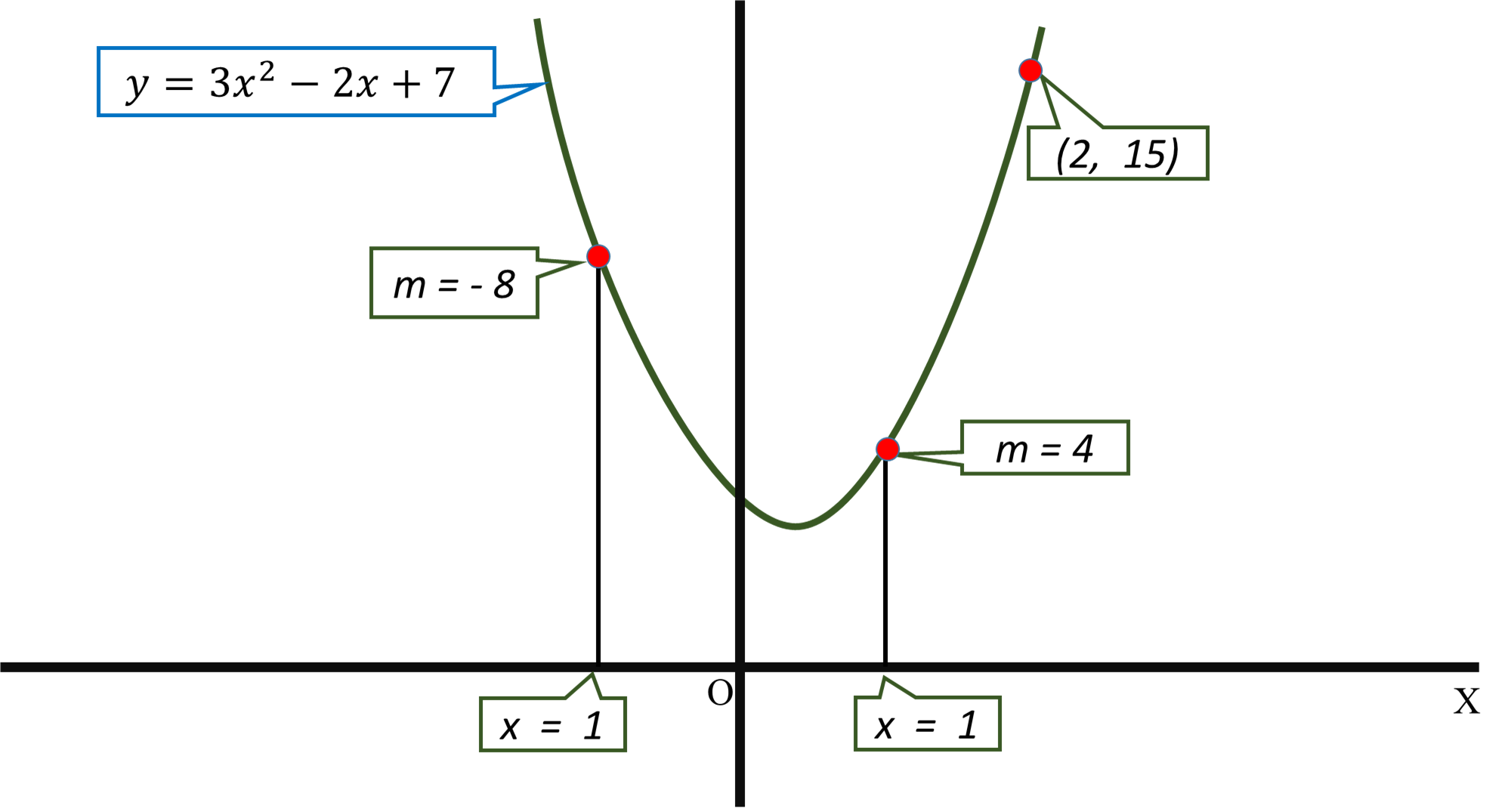



How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic




8 3 Graphing F X Ax 2 Bx C Youtube



Parabolas



Graphing Quadratic Functions The Leading Coefficient The Vertex



Show That Y Ax 2 Bx C A 0 Represents A Parabola And Find Its Vertex Focus Directrix And Latus Rectum Sarthaks Econnect Largest Online Education Community
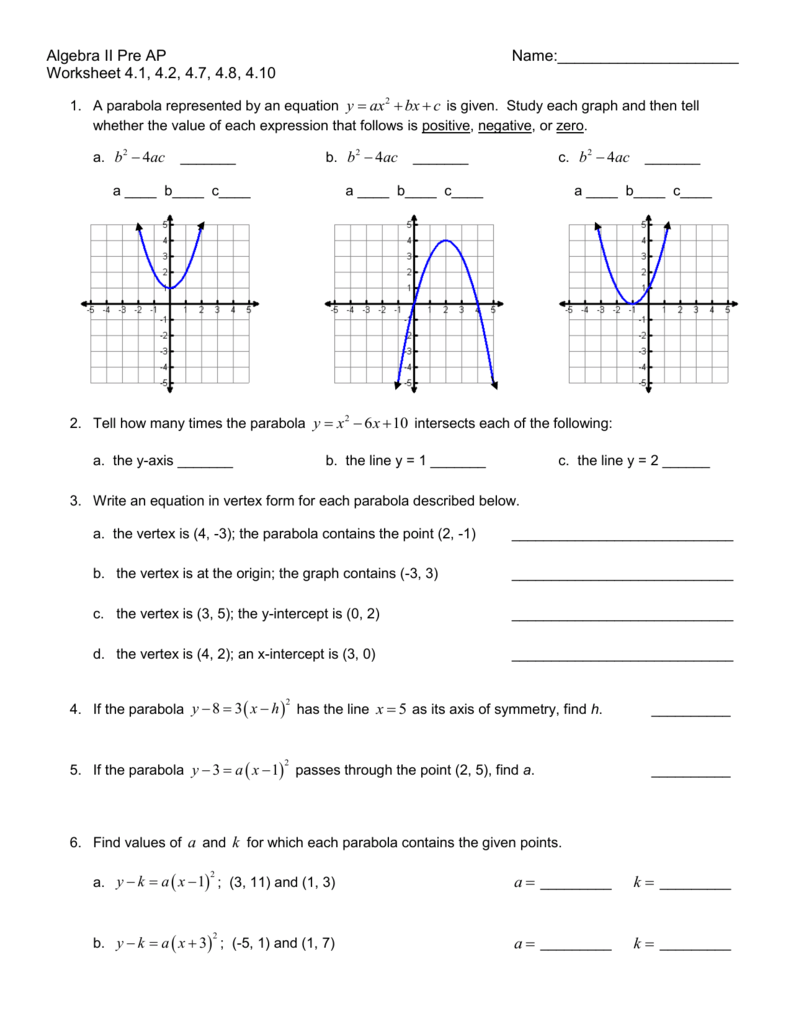



H Gt Algebra 2 Worksheet 4



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Which Of The Following Is An Equation In The Form Y Ax2 Bx C Of The Parabola Shown In The Brainly Com



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego Flip Ebook Pages 1 5 Anyflip Anyflip




Quadratic Function



Vertex Directrix And Focus Of Quadratic Equations




The Graphs Of Y Ax 2 Bx C Are Given In Figure Identify The Signs Of A B And C In Each Of The Following



What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora
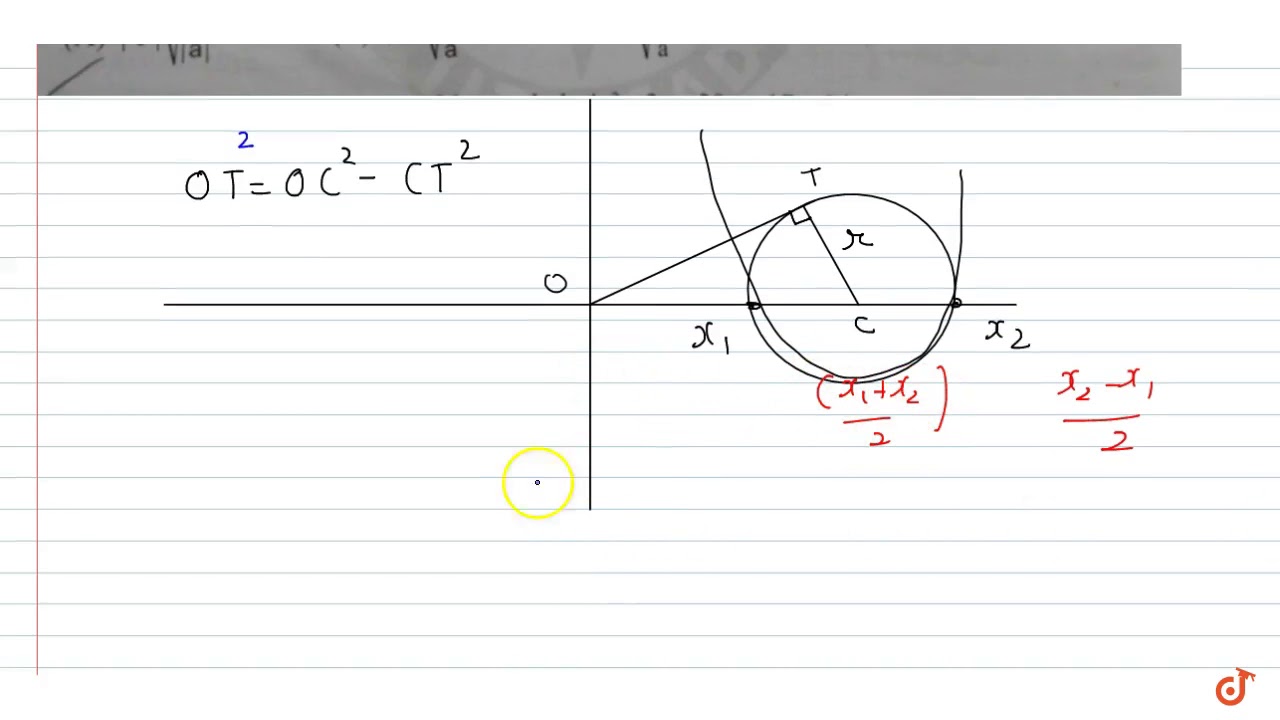



A Parabola Y Ax 2 Bx C Ac Gt 0 Crosses The X Axis At A And B A Variable Circle Is Dra Youtube




Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Then Which Of The Following Is True



Unique Quadratic Equation In The Form Y Ax 2 Bx C



Vertex And Intercepts




How To Find The Vertex Of A Quadratic Equation Video Lesson Transcript Study Com
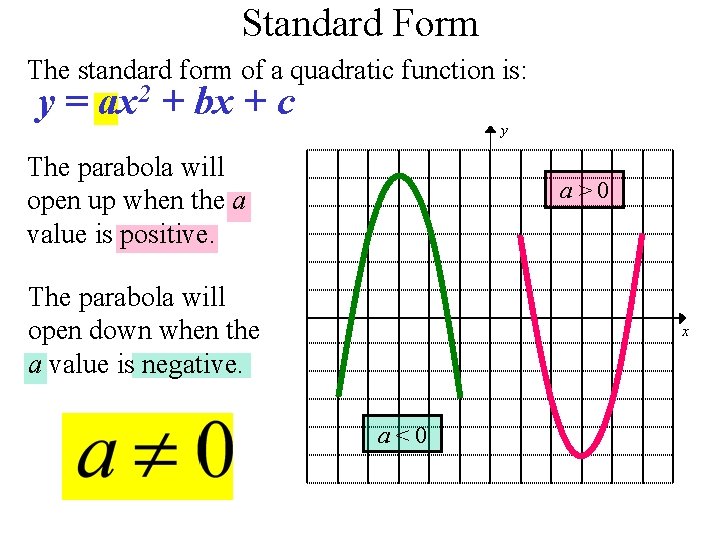



Quadratic Function Y Ax 2 Bx C Quadratic




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



0 件のコメント:
コメントを投稿